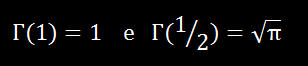A função gama foi definida por Euler por meio da integral
Existe uma relação de recorrência para esta função, que pode ser obtida por integral por partes. Além disto, a convergência da integral requer x - 1 > -1 ou x > 0. Por integral por partes, fazendo
temos que
Perceba que
Assim,
Lembrando que
temos então que
que é equivalente a
Esta é a definição mais comum da função gama. Vemos que, para qualquer n inteiro positivo,
Por essa razão, a função gama é frequentemente chamada função fatorial generalizada. Dois resultados muito importantes são
Referências
ZILL, D. G. Equações diferenciais com aplicações em modelagem. Tradução Cyro de Carvalho Patarra; revisão técnica Antônio Luiz Pereira. São Paulo: Pioneira Thomson Learning, 2003.